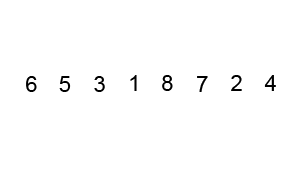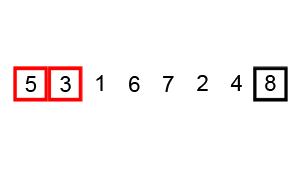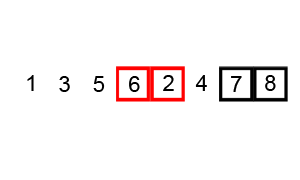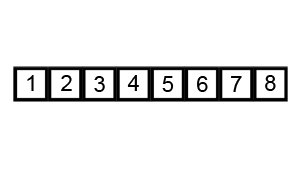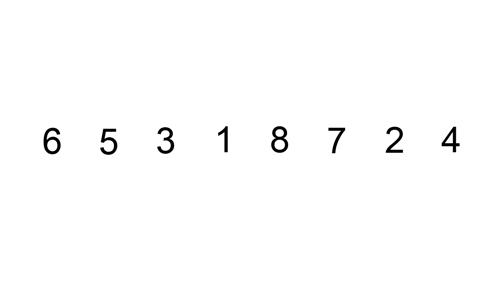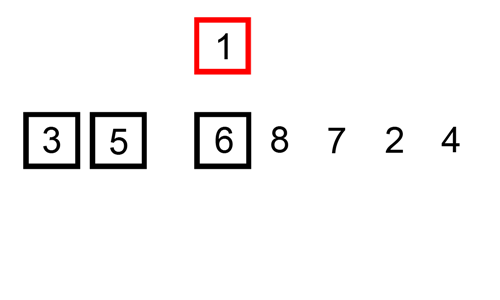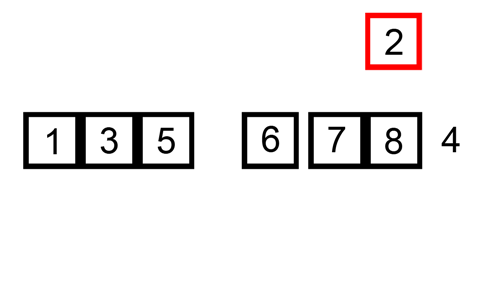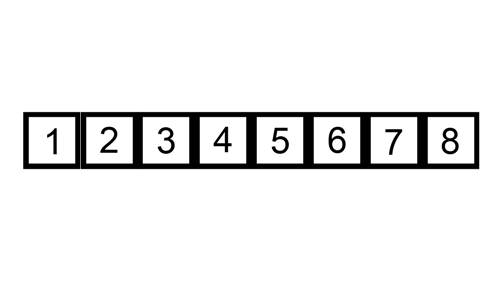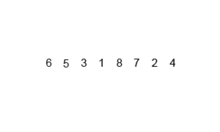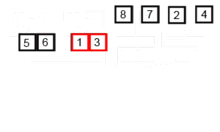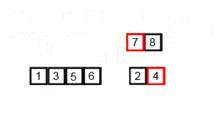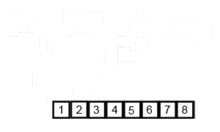정렬 알고리즘 정리

정렬이란?

• 정렬 (sorting): 어떤 데이터들이 주어졌을 때 정해진 순서대로 나열하는 것
• 프로그래밍에서 자주 사용됨
• 정렬을 위한 다양한 알고리즘이 있음

+빅오 비교 (Big O)

O(1) < O(log n) < O(n) < O(n*log n) < O(n^2) < O(2^n) < O(n!)

쉬운 설명을 위해 모든 예시는 오름차순 정렬을 사용함

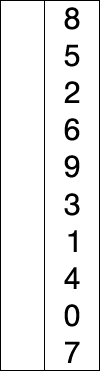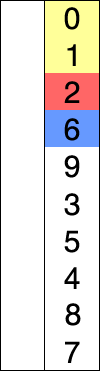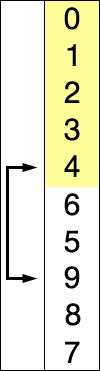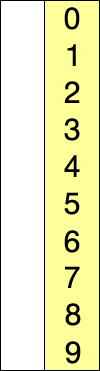
버블정렬 (Bubble sort)

• 인접한 두 데이터를 비교
• 앞에 있는 데이터가 뒤에 있는 데이터보다 크면 Swap!
• 시간복잡도: O(n^2)

이미지 출처

def bubbleSort(x):
  length = len(x)-1
  for i in range(length):
    for j in range(length-i):
      if x[j] > x[j+1]:		# 앞에가 더 크면 Swap
        x[j], x[j+1] = x[j+1], x[j]
  return x

삽입정렬 (Insertion sort)

• 앞에 있는 데이터들과 비교
• 비교할 데이터보다 작은 데이터가 나오는 곳에 Insert!
• O(n^2)

이미지 출처

def insert_sort(x):
  for i in range(1, len(x)):
    j = i - 1
    key = x[i]
    while x[j] > key and j >= 0:	#자신보다 크면 순서 바꾸기
      x[j+1] = x[j]
      j = j - 1
      x[j+1] = key			# 반복문 멈춘 자리에 Insert
  return x

선택정렬 (Selection sort)

• 데이터 중 최소값을 찾아 맨 앞과 Swap
• O(n^2)

이미지 출처

def selectionSort(x):
  length = len(x)
  for i in range(length-1):
    indexMin = i
    for j in range(i+1, length):
      if x[indexMin] > x[j]:
        indexMin = j			#최소값 찾기
      x[i], x[indexMin] = x[indexMin], x[i]	#맨 앞과 Swap
  return x

병합정렬 (Merge sort)

• 재귀 활용 (분할 정복) <-아래 설명 확인
• 절반으로 잘게 자르고 다시 합병하며 정렬
• O(n*log n)

이미지 출처

def split(data_list):
  if len(data_list) <= 1:	#탈출: 더 자를수 없음
    return data_list

  mid = len(data_list) // 2	#가운데를 기준으로 나눠서 재귀
  left = split(data_list[:mid])
  right = split(data_list[mid:])
  return merge(left, right)	#병합

def merge(left, right):
  merged = list()
  left_i, right_i = 0, 0

  while left_i<len(left) and right_i<len(right):
    if right[right_i] < left[left_i]:    #left, right 중 작은 값 하나씩 추가
      merged.append(right[right_i])
      right_i += 1
    else:
      merged.append(left[left_i])
      left_i += 1

  #남은 값들 추가
  while left_i < len(left):
    merged.append(left[left_i])
    left_point += 1
  while right_i < len(right):
    merged.append(right[right_i])
    right_i += 1

  return merged

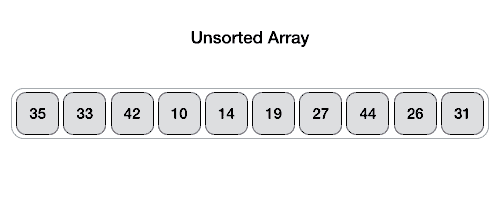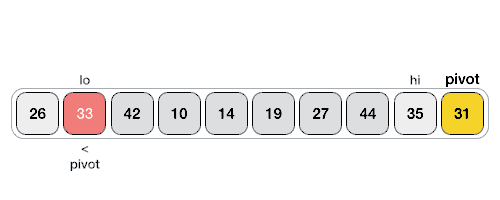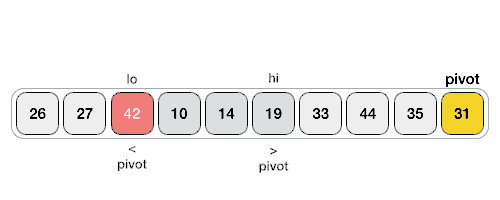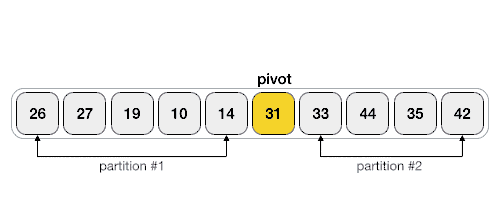
퀵정렬 (Quick sort)

• 기준(pivot)을 잡고 해당 값보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 Swap
• 기준을 잡는 방법은 다양함
• O(n*log n)
• 정렬 알고리즘의 꽃 (이름부터 빨라)

이미지 출처

def quicksort(x):
  if len(x) <= 1:		#탈출: 더 자를 수 없음
    return x
  pivot = x[len(x) // 2]	#인덱스 기준 중간값을 기준점으로
  less = []
  more = []
  equal = []
  for a in x:			#모든 값을 기준값과 비교해 3개의 그룹으로 나눔
    if a < pivot:
      less.append(a)
    elif a > pivot:
      more.append(a)
    else:
      equal.append(a)
  return quicksort(less) + equal + quicksort(more)	#재귀 및 병합

---

* 동적 계획법 & 분할 정복

추가로 알아보면 좋을 내용 :)

a. 동적 계획법 (Dynamic Programming)

• 흔히 DP라고 불림
• 상향식 접근법: 최하위 해답을 구한 후 이를 이용해 상위 문제를 풀어가며 결국 전체 문제를 해결
• Memoization 기법 사용: 이전에 계산한 값을 저장
• 피보나치 수열 등

b. 분할 정복 (Divide and Conquer)

• 하향식 접근법: 문제를 최대한 나누어 풀고 다시 합병하여 전체 문제를 해결
• Memoization 기법 사용 X
• 퀵 정렬 등