그래프와 DFS, BFS 정리

그래프 (Graph)

그래프란?

• 여러 노드와 간선으로 연결된 네트워크 또는 자료구조
• 그래프(Graph)는 노드(Vertex)와 간선(Edge)으로 이루어짐 G = (V, E)
• 차수(Degree)는 해당 노드에 연결된 간선의 수

그래프 종류

• 무방향 그래프 / 방향 그래프: 간선에 방향이 있거나 없음
• 가중치 그래프: 간선에 비용이 할당됨
• 완전 그래프: 모든 노드가 서로 연결됨
• 비연결 그래프 / 연결 그래프
• 순환 그래프 / 비순환 그래프

들어가기 전 DFS vs BFS 간단비교

이미지 출처

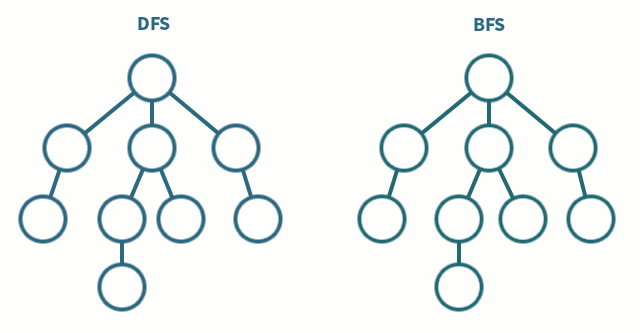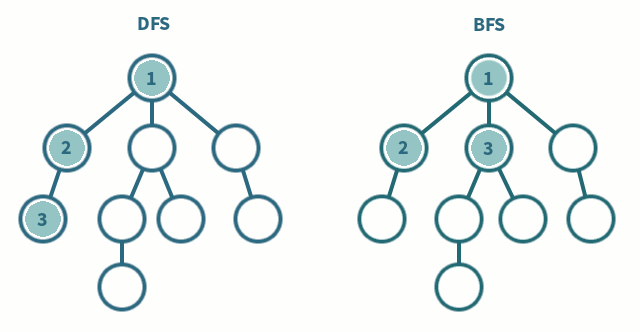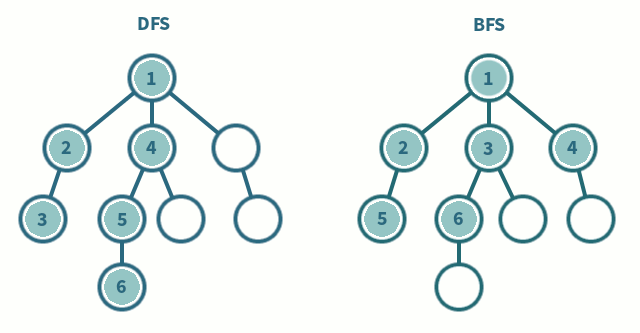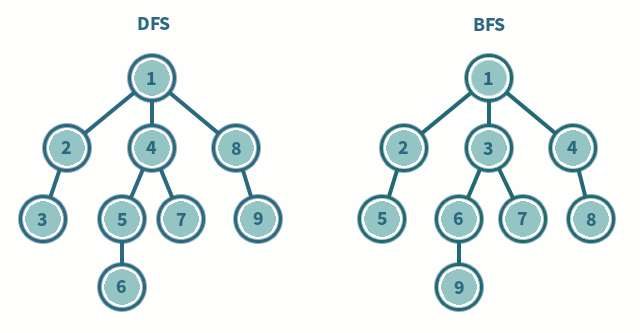
깊이우선탐색 (Depth First Search)

• 한 노드의 자식을 끝까지 순회한 후 다른 노드 순회
• 자식 우선
• 스택(LIFO) 사용

너비우선탐색 (Breadth First Search)

• 한 단계씩 내려가면서 같은 레벨에 있는 노드들을 먼저 순회
• 형제 우선
• 큐(FIFO) 사용

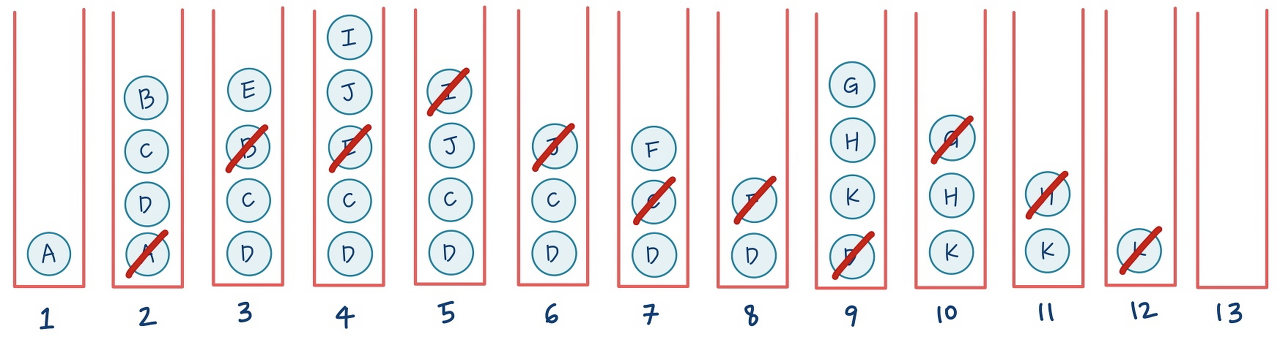
깊이 우선 탐색 (DFS)

DFS에서는 한 단계에서 Pop과 Extand를 수행 (LIFO)

1. Pop: 스택의 맨 위 노드를 꺼냄
2. Extand: 지워진 노드의 자식들을 모두 스택에 넣음

이미지 출처

def DFS(start_node, target_node):
	# 1) stack 에 첫 번째 노드 넣으면서 시작
	stack = [start_node, ]
    
	while True:
		# 2) stack이 비어있으면 종료
		if len(stack) == 0:
			print("None")
			return None
            
		# 3) stack에서 맨 뒤의 노드를 pop
		node = stack.pop()

		# 4) target_node를 찾으면 해당 노드 반환 (조건문은 상황에 따라 다름)
		if node == target_node:
			print('The target found.')
			return node

		# 5) node의 자식을 expand 해서 childrens에 저장
		childrens = expand(node)

		# 6) childrens을 stack에 넣기
		stack.extend(childrens)

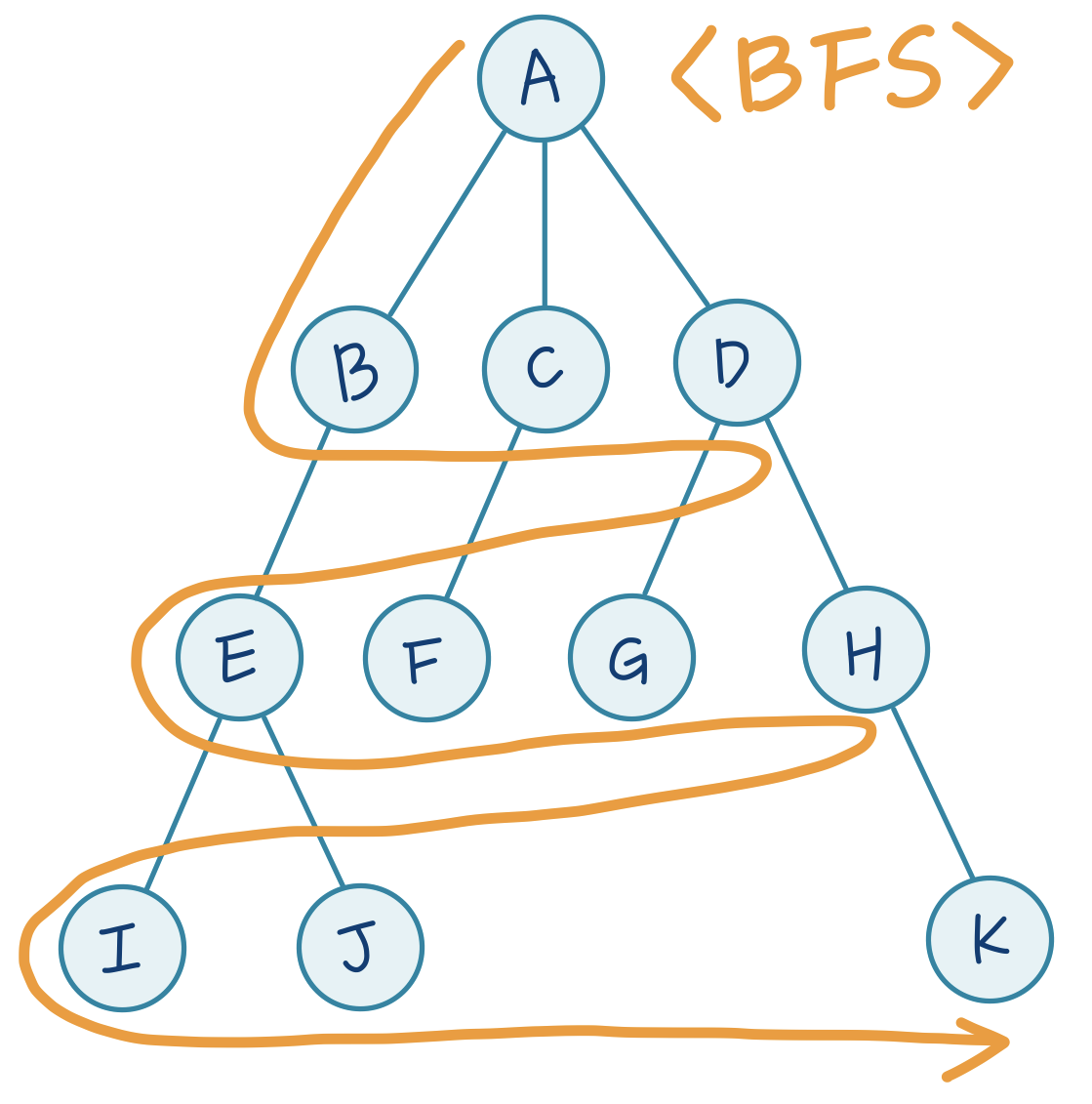
넓이 우선 탐색 (BFS)

BFS에서는 한 단계에서 Dequeue과 Enqueue를 수행 (FIFO)

1. Dequeue: 큐의 맨 위 노드를 꺼냄
2. Enqueue: 지워진 노드의 자식들을 모두 스택에 넣음

이미지 출처

def BFS(start_node, target_node):
	# 1) queue 에 첫 번째 노드 넣으면서 시작
	queue = [start_node, ]

	while True:
		# 2) queue가 비어있으면 종료
		if len(queue) == 0:
			print('None')
			return None
                
		# 3) queue에서 맨 위의 노드를 dequeue (0번 인덱스를 pop)
		node = queue.pop(0)
                
		# 4) target_node를 찾으면 해당 노드 반환 (조건문은 상황에 따라 다름)
		if node == target_node:
			print('The target found.')
			return node

		# 5) node의 자식을 expand 해서 childrens에 저장
		childrens = expand(node)

		# 6) childrens을 queue에 넣기
		queue.extend(children)

요약

구분	DFS	BFS
우선순위	자식먼저(깊게)	형제먼저(넓게)
자료구조	스택(LIFO)	큐(FIFO)
코드차이 (위 코드 기준)	pop()	pop(0)